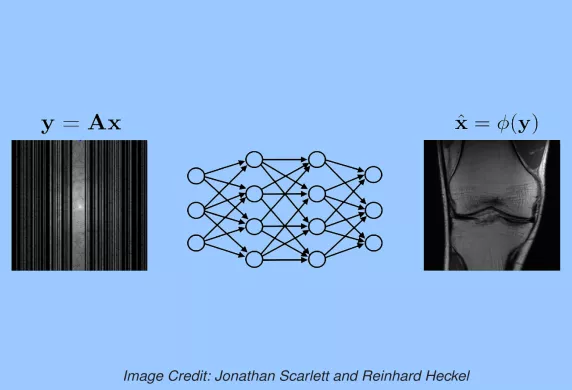
Deep learning methods have emerged as highly successful tools for solving inverse problems. They achieve state-of-the-art performance on tasks such as image denoising, inpainting, super-resolution, and compressive sensing. They are also starting to be used in inverse problems beyond imaging, including for solving inverse problems arising in communications, signal processing, and even on non-Euclidean data such as graphs. However, a wide range of important theoretical and practical questions remain unsolved or even completely open, including precise theoretical guarantees for signal recovery, robustness and out-of-distribution generalization, architecture design, and domain-specific applications and challenges. This special issue aims to advance cutting-edge research in this area, with an emphasis on its intersection with information theory.
Reed-Muller (RM) codes achieve the capacity of general binary-input memoryless symmetric channels and are conjectured to have a comparable performance to that of random codes in terms of scaling laws. However, such results are established assuming maximum-likelihood decoders for general code parameters. Also, RM codes only admit limited sets of rates. Efficient decoders such as successive cancellation list (SCL) decoder and recently-introduced recursive projection-aggregation (RPA) decoders are available for RM codes at finite lengths. In this paper, we focus on subcodes of RM codes with flexible rates. We first extend the RPA decoding algorithm to RM subcodes. To lower the complexity of our decoding algorithm, referred to as subRPA, we investigate different approaches to prune the projections. Next, we derive the soft-decision based version of our algorithm, called soft-subRPA, that not only improves upon the performance of subRPA but also enables a differentiable decoding algorithm. Building upon the soft-subRPA algorithm, we then provide a framework for training a machine learning (ML) model to search for good sets of projections that minimize the decoding error rate. Training our ML model enables achieving very close to the performance of full-projection decoding with a significantly smaller number of projections. We also show that the choice of the projections in decoding RM subcodes matters significantly, and our ML-aided projection pruning scheme is able to find a good selection, i.e., with negligible performance degradation compared to the full-projection case, given a reasonable number of projections.
